Buscar

Funciones

Admin
28 feb 2017
3 Min. de lectura

En este curso de Matemáticas IV, Cálculo Diferencial e Integral, hablaremos mucho sobre funciones, límites, derivadas, continuidad y aplicaciones de éstas para la resolución de problemas matemáticos y la creación de proyectos aplicando los temas vistos.

En este caso, una función es una relación entre dos conjuntos en la cual a cada elemento del primer conjunto le corresponde UNO y SOLAMENTE UNO de los elementos del segundo conjunto.

En este ejemplo, tenemos que el Conjunto 1 no cumple con la regla para que sea una función. En el primer caso, el conjunto 1 el último valor "U" está unido a dos elementos del segundo conjunto; mientras que en el segundo caso, el último valor "U" no está unido a ningún elemento, por lo tanto es una Relación.

En este caso sí es una función ya que cumple con lo anteriormente establecido.

El primer conjunto lo llamaremos dominio mientras que el segundo conjunto lo llamaremos rango.

En el ejemplo establecido en la imagen anterior, al tener claro la definición de función veremos lo que significa la regla de correspondencia, que como dice, es una ecuación que nos permite asignar un elemento del dominio con alguno otro del rango.

El primer conjunto, los elementos del dominio serán nuestros valores en x, mientras que en el segundo conjunto, lo elementos del rango serán nuestros valores en y.

En el ejemplo mostrado en la tabla, los primeros 4 valores tienen un valor asignado:

Para 1 = 3

Para 2 = 5

Para 3 = 7

Para 4 =9

En el caso de 5 = ?

Debemos hallar la secuencia que siguen los valores de los elementos del rango para saber cuál es el siguiente valor del mismo, en este caso la ecuación es y=2x+1.

Al momento de tener nuestra ecuación, una función se lee como "efe de x" o "función de x".

Los valores en Y son conocidos como nuestra variable dependiente, mientras que los valores en X son conocidos como variable independiente.

En este ejemplo cuando nuestra función de x es igual a 4x-3 debemos hallar los valores que se muestran en la imagen. Para hacerlo, sustituimos el valor que queremos hallar (0) (-1) (x+h) (x-h) etc... como se muestra.

Lo que nos queda que cuando f(x)=4x-3, entonces f(0) = 4(0) - 3 que esto es igual a -3.

Como se muestra en la imagen cuando f(x)=√x-5 nos piden hallar f(0)

al hacer la sustitución en x nos queda f(0) =√0-5 lo que nos deja como √-5, por lo tanto es imaginaria, asi como si sustituyéramos algún valor negativo o hasta el 4, nuestro resultado será imaginario, esto cambia cuando nuestro valor en x llega a 5, si seguimos sustituyendo valores obtendremos resultados, ya sean positivos o negativos. Los valores sustituidos en x son nuestro dominio, mientras que los valores que obtengamos al hacer la sustitución en nuestra función serán nuestro rango.

Como explica la imagen nuestro Dominio de la función (Df) indica los valores con los que se cumple la función al sustituir los valores en x, mientras que el Rango de la función (Rf) son nuestros posibles resultados, positivos o negativos.

Tanto en el caso del Dominio y el Rango de nuestra función para indicar nuestros valores utilizamos los símbolos ( ) y [ ].

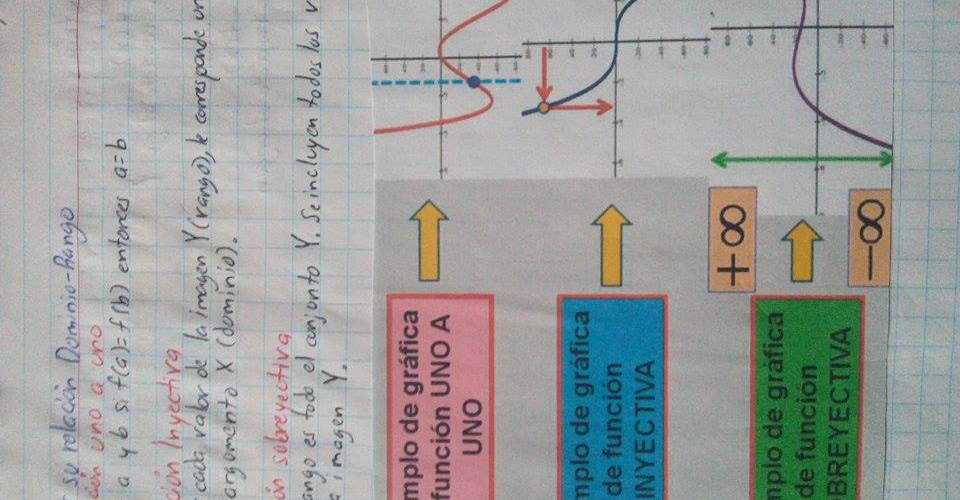
Al utilizar los símbolos de paréntesis ( ) estamos indicando que nuestro dominio o rango de la función no se incluyen los valores que se encuentren en medio de éstos, como se explica en la imagen, ( 0, ∞) quiere decir que no se toman en cuenta los valores del 0 ni el infinito, es decir, se tomarán en cuenta los valores arriba de 0 y menores a ∞; en el segundo ejemplo [-∞,∞] se incluyen los valores tanto del infinito negativo como el positivo; en el último ejemplo [5,∞) el valor del 5 se incluye hasta el infinito, mientras que este último no se toma en cuenta.